2021-12-27

关于深度优先搜索

什么是深度优先搜索？

深度优先搜索（DFS）是与广度优先搜索想对应的算法，它的思想是从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底，这种尽量往深处走的概念即是深度优先的概念。

深度优先搜索适用于哪些场景？

深度优先搜索算法适用场景是在数组、图、树…等数据结构中，查询符合条件的解，虽是比较暴力的搜索算法，但因为只求有解，所以消耗比较小，深度优先搜索算法是联合回溯的算法思想，可以使用递归来实现，

场景1 二叉树

给定二叉搜索树（BST）的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */
function searchBST(root: TreeNode | null, val: number): TreeNode | null {
    let searchedNode: TreeNode | null = null;
    let dfs = function (node:  TreeNode | null) {
        // 边界条件
        // 完成条件
        if (node === null||searchedNode) {
            return; // 弹出所有栈
        }
        console.log(node.val); // 打印节点值
        // 业务判断
        if(node.val === val){
          searchedNode = node;
          return;  // 弹出当前栈
        }
        dfs(node.left);
        dfs(node.right);
    }
    dfs(root);
    return searchedNode;
}

以上就是一个最简洁的深度优先搜索的样本，给定二叉搜索树（BST）的根节点和一个值,需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。

假设树为下图，需要查找的目标值为7

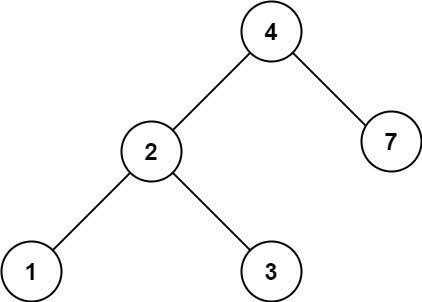
那么输出值的顺序应该是深度优先，如4、2、1、3，7，弹出

场景2

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按任何顺序返回答案。

示例：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

function combine(n: number, k: number): number[][] {
    // 准备返回的资源
    const ans: number[][] = [];
    // 临时数组
    const temp: number[] = [];

    const dfs = (cur: number,n: number,k: number) => {
        // 当临时数组的长度等于k，满足一个组合条件，推送到资源中，并弹出当前栈
        if(temp.length === k){
            ans.push([...temp]);
            return;
        }
        // 当前的数已经到达递归边界，弹出栈
        if(cur === n + 1){
            return;
        }
        // 将当前数推送到临时数组
        temp.push(cur);
        // 深度搜索
        dfs(cur + 1,n,k);
        // 回溯，当执行到此，说明上一个栈已经在第89行弹出，所以临时数组弹出一个元素，再次进行深度搜索
        temp.pop();
        // 深度搜索
        dfs(cur + 1,n,k);
    }

    dfs(1,n,k);
    return ans;
}

场景3

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。叶子节点是指没有子节点的节点。

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function hasPathSum(root: TreeNode | null, targetSum: number): boolean {
    // 预设结果 false
    let result: boolean = false;
    // 是否已经结束 false
    let isEnd: boolean = false;

    // 如果根节点为null则直接弹出false
    if (!root) {
        return false;
    }

    // 如果根节点的值等于目标和，且自身也是叶子节点时，返回true
    if (root.val === targetSum) {
        if (!root.left && !root.right) {
            return true;
        }
    }


    // 深度优先搜索
    const dfs = (node: TreeNode | null, sum: number, prevSum: number) => {
        // 如果当前节点为null，则将求和回溯到上一个和，弹出当前栈
        if (!node) {
            sum = prevSum;
            return;
        }
        // 如果已经结束，弹出当前栈
        if (isEnd) {
            return;
        }
        // 如果和等于目标值，且当前节点是叶子节点，则声明结果为true，且声明已经结束，且弹出当前栈
        if (sum === targetSum) {
            if (!node.left && !node.right) {
                result = true;
                isEnd = true;
                return;
            }
        }
        // 优先搜索左树，将左树的求和进行入参，将当前和以上一步和的名义入参
        dfs(node.left, sum + (node.left?.val ?? 0), sum);
        // 当左树达到边界条件弹出，则将右树进行入栈递归
        dfs(node.right, sum + (node.right?.val ?? 0), sum);
    }

    dfs(root, root.val, 0);

    return result;
};

关于此算法的心得

深度优先搜索是一个算法思想，在方法体中注意三个边界条件

被搜索的对象集合已经用完-弹出栈，
已经完成目标-弹出栈
满足搜索条件，声明已经完成目标，弹出栈

在进行递归栈的时候，应以深度进行优先，往深处将递归语句进行入栈，如果没有搜索到，再进行回溯，然后进行深度搜索

2021-10-10

设计循环队列

解题思路

队列是遵行先进先出的策略，而循环队列则使用固定大小的数组，使得队列在数组未空的情况下，绕行数组添加元素或删除元素，采用双指针来指示不断变化的头部与尾部，目的是未了节省内存的空间。

2021-09-25

ts的类型系统

接口

TypeScript的核心原则之一是对值所具有的_结构_进行类型检查。它有时被称做“鸭式辨型法”或“结构性子类型化”。在 TypeScript 里，接口的作用就是为这些类型命名和为你的代码或第三方代码定义契约。

2021-09-19

命令模式

命令模式把一个请求或者操作封装到一个对象中。命令模式允许系统使用不同的请求把客户端参数化，对请求排队或者记录请求日志，可以提供命令的撤销和恢复功能

2021-09-06

外观模式

外观（Facade）模式又叫作门面模式，是一种通过为多个复杂的子系统提供一个一致的接口，而使这些子系统更加容易被访问的模式。该模式对外有一个统一接口，外部应用程序不用关心内部子系统的具体细节，这样会大大降低应用程序的复杂度，提高了程序的可维护性。


// 子系统A
class SubSystemA{
  print(){
    console.log('i am subsystem A');
  }
}

// 子系统B
class SubSystemB{
  say(){
    console.log('i am subsystem B');
  }
}

// 外观类
class System{
  private sa: SubSystemA = new SubSystemA();
  private sb: SubSystemB = new SubSystemB();
  print(){
    this.sa.print();
  }
  say(){
    this.sb.say();
  }
}

(function main(){
  const sy = new System();
  sy.print();
  sy.say();
})()

采用外观模式，使得客户端与子系统不在紧耦，而是通过外观类进行统一的业务处理

2021-08-22

组合模式

组合模式（Composite Pattern），又叫部分整体模式，是用于把一组相似的对象当作一个单一的对象。组合模式依据树形结构来组合对象，用来表示部分以及整体层次。这种类型的设计模式属于结构型模式，它创建了对象组的树形结构。

2021-08-21

桥接模式

分离抽象接口及其实现部分。桥接模式使用”对象间的关联关系”解耦了抽象和实现之间固有的绑定关系，使得抽象和实现可以沿着各自的维度来变化。所谓抽象和实现沿着各自维度的变化，也就是说抽象和实现不再在同一个继承层次结构中，而是”子类化”它们，使它们各自都具有自己的子类，以便任何组合子类，从而获得多维度组合对象。

2021-08-15

适配器模式

适配器模式可以是一个类，将需要适配的对象进行成员实例化，同时继承原对象，在保持原对象原方法接口不变的情况下，覆写原方法，调用成员实例的方法实现新的功能

见代码

2021-05-22

判断二叉树是否为一个平衡二叉树

见代码

const height = (node: TreeNode):number => {
    if(node===null){
        return 0;
    }
    return Math.max(height(node.left),height(node.right)) + 1;
}

function isBalanced(root: TreeNode | null): boolean {
    if(root===null){
        return true;
    }
    return Math.abs(height(root.left) - height(root.right)) <=1 && isBalanced(root.left) && isBalanced(root.right);
};

2021-05-02

将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过1」的二叉树。

重影对话

Jonny Peng's personal blog

关于深度优先搜索

什么是深度优先搜索？

深度优先搜索适用于哪些场景？

场景1 二叉树

场景2

场景3

关于此算法的心得

设计循环队列

解题思路

ts的类型系统

接口

命令模式

外观模式

组合模式

桥接模式

适配器模式

判断二叉树是否为一个平衡二叉树

将有序数组转换为二叉搜索树